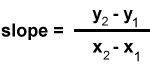Chapter Three: Parallel And Perpendicular Lines
Section One: Lines And Angles
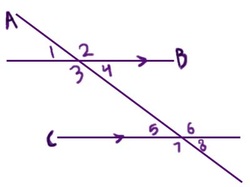
Figure A
_Transversal: A line that intersects two coplanar lines at two different points.
Alternate exterior angles: For two lines intersected by a transversal, a pair of angles that lie on opposite sides of the transversal and outside the other two lines.
Alternate interior angles: For two lines intersected by a transversal, a pair of nonadjacent angles that lie on opposite sides of the transversal and between the other two lines.
Corresponding Angles: For two lines intersected by a transversal, a pair of angles that are on the same side of the transversal and on the same side of the other two lines
Parallel lines:Lines in the same plane that do not intersect.
Parallel planes: Planes that do not intersect.
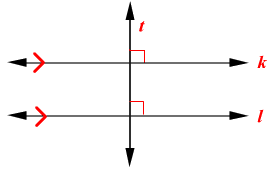
Perpendicular lines:Lines that intersect at 90 angles.
Same-side interior angles:For two lines intersected by a transversal, a pair of angles that lie on the same side of the transversal and between the two lines.
Skew lines: Lines that are not coplanar.
In figure A:
<1 and <5 are corresponding angles.
<1 and <8 are alternate exterior angles.
<4 and < 5 are alternate interior angles.
<4 and <6 are same-side interior angles.
Alternate exterior angles: For two lines intersected by a transversal, a pair of angles that lie on opposite sides of the transversal and outside the other two lines.
Alternate interior angles: For two lines intersected by a transversal, a pair of nonadjacent angles that lie on opposite sides of the transversal and between the other two lines.
Corresponding Angles: For two lines intersected by a transversal, a pair of angles that are on the same side of the transversal and on the same side of the other two lines
Parallel lines:Lines in the same plane that do not intersect.
Parallel planes: Planes that do not intersect.
Perpendicular lines:Lines that intersect at 90 angles.
Same-side interior angles:For two lines intersected by a transversal, a pair of angles that lie on the same side of the transversal and between the two lines.
Skew lines: Lines that are not coplanar.
In figure A:
<1 and <5 are corresponding angles.
<1 and <8 are alternate exterior angles.
<4 and < 5 are alternate interior angles.
<4 and <6 are same-side interior angles.
Section Two: Angles Formed By Parallel lines and Transversals
Postulate 3-2-1 (corresponding angles postulate): If two parallel lines are cut by a transversal, then the pair of corresponding angles are congruent.
Theorem 3-2-2 (alternate interior angles theorem):If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent.
Theorem 3-2-3 (alternate exterior angles theorem): If two parallel lines are cut by a transversal, then the two pairs of alternate exterior angles are congruent.
Theorem 3-2-4 (same-side interior angles theorem): If two parallels are cut by a transversal, then the two pairs of same side interior angles are congruent.
Theorem 3-2-2 (alternate interior angles theorem):If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent.
Theorem 3-2-3 (alternate exterior angles theorem): If two parallel lines are cut by a transversal, then the two pairs of alternate exterior angles are congruent.
Theorem 3-2-4 (same-side interior angles theorem): If two parallels are cut by a transversal, then the two pairs of same side interior angles are congruent.
Section Three: Proving Lines Are Parallel
Postulate 3-3-1 (Converse of the corresponding Angles): If two coplanar lines are cut by a transversal so that a pair of corresponding angles are congruent, then the two lines are parallel.
Postulate 3-3-2 (Parallel Postulate)- Through a point P not on a line L, there is exactly one line parallel to L.
Theorem 3-3-3 (Converse of the Alternate Interior Angles Theorem): If two coplanar lines are cut by a transversal so that a pair of alternate interior angles are congruent, then the two lines are parallel.
Theorem 3-3-4 (Converse of the Alternate Exterior Angles Theorem): If two coplanar angles are cut by a transversal so that a a pair of same-side interior angles are supplementary, then the two lines are parallel.
Postulate 3-3-2 (Parallel Postulate)- Through a point P not on a line L, there is exactly one line parallel to L.
Theorem 3-3-3 (Converse of the Alternate Interior Angles Theorem): If two coplanar lines are cut by a transversal so that a pair of alternate interior angles are congruent, then the two lines are parallel.
Theorem 3-3-4 (Converse of the Alternate Exterior Angles Theorem): If two coplanar angles are cut by a transversal so that a a pair of same-side interior angles are supplementary, then the two lines are parallel.
Section Four: Perpendicular Lines
Perpendicular bisector: A line perpendicular to a segment at the segment’s midpoint.
Distance from a point to a line: The length of the perpendicular segment from the point to the line.
Theorem 3-4-1: If two intersecting lines form a linear pair of congruent angles, then the lines are perpendicular.
Theorem 3-4-2 (Perpendicular Transversal Theorem): In a plane, if a transversal is perpendicular to one of two parallel lines, then it is perpendicular to the other line.
Theorem 3-4-3: If two coplanar lines are perpendicular to the same line, then the two lines are parallel to each other.
Distance from a point to a line: The length of the perpendicular segment from the point to the line.
Theorem 3-4-1: If two intersecting lines form a linear pair of congruent angles, then the lines are perpendicular.
Theorem 3-4-2 (Perpendicular Transversal Theorem): In a plane, if a transversal is perpendicular to one of two parallel lines, then it is perpendicular to the other line.
Theorem 3-4-3: If two coplanar lines are perpendicular to the same line, then the two lines are parallel to each other.
Section Five: Slopes Of Lines
Rise: The difference in the y-values of two points on a line. -values of two points on a line.
Run: The difference in the x-values of two points on a line. -values of two points on a line.
Slope: A measure of the steepness of a line. If (x1, y1) and (x2, y2) are any two points on the line, the slope of the line, known as m, is represented by the equation m = y2 - y1 over x2 - x1.
Theorem 3-5-1 (Parallel lines Theorem): In a coordinate planes, two nonvertical lines are parallel if and only if they have the same slope. Any two vertical lines are parallel.
Theorem 3-5-2 (Perpendicular Lines Theorem): In a coordinate planes, two nonvertical lines are parallel if and only if the product of their slopes is -1. Vertical and horizontal lines are perpendicular.
Run: The difference in the x-values of two points on a line. -values of two points on a line.
Slope: A measure of the steepness of a line. If (x1, y1) and (x2, y2) are any two points on the line, the slope of the line, known as m, is represented by the equation m = y2 - y1 over x2 - x1.
Theorem 3-5-1 (Parallel lines Theorem): In a coordinate planes, two nonvertical lines are parallel if and only if they have the same slope. Any two vertical lines are parallel.
Theorem 3-5-2 (Perpendicular Lines Theorem): In a coordinate planes, two nonvertical lines are parallel if and only if the product of their slopes is -1. Vertical and horizontal lines are perpendicular.
Section Six: Lines In The Coordinate Plane
Point-slope form: y -y1 =m(x- x1), where m is the slope and (x1 y1) is a point on the line.
Slope Intercept form: The slope-intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept.
Slope Intercept form: The slope-intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept.