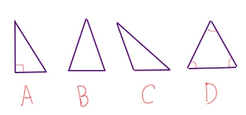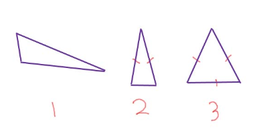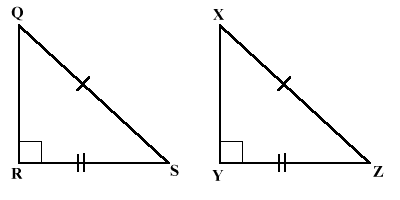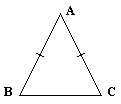Chapter Four: Triangle Congruence
Section One: Classifying Triangles
Triangle: A polygon with three sides. The measures of it’s angles add up to 180.
Acute Triangle: A triangle with three acute angles. (A)
Right Triangle: A triangle with one right angle and two acute angles. (B)
Obtuse Triangle: A triangle with one obtuse angle and two acute angles. (C)
Equiangular Triangle: A triangle with three congruent angles. (D)
Scalene Triangle: A triangle with no congruent sides. (1)
Isosceles Triangle: A triangle with two congruent sides. (2)
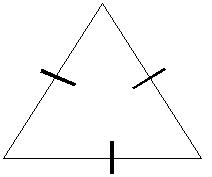
Equilateral Triangle: A triangle with three congruent sides. (3)
Acute Triangle: A triangle with three acute angles. (A)
Right Triangle: A triangle with one right angle and two acute angles. (B)
Obtuse Triangle: A triangle with one obtuse angle and two acute angles. (C)
Equiangular Triangle: A triangle with three congruent angles. (D)
Scalene Triangle: A triangle with no congruent sides. (1)
Isosceles Triangle: A triangle with two congruent sides. (2)
Equilateral Triangle: A triangle with three congruent sides. (3)
Section Two: Angle Relations in Triangles
Triangle Sum Theorem: The sum of the angle measures of a triangle is 180 degrees. Angle A + Angle B+ Angle C= 180 degrees.
Auxiliary line is a line that is added to a figure to aid in a proof.
Corollary:
4-2-2: The acute angles of a right triangle are complementary.
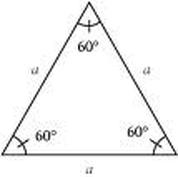
4-2-3: The measure of each angle of a equiangular triangle is 60 degrees.
Example: One of the acute angles in a right triangle measures 22.9 degrees. What is the measure of the other acute angle? 22.9+m=90 m=67.1.
Interior is the set of all points inside the figure.
Exterior is the set of all points outside the figure.
Interior angle is formed by two sides of a triangle.
Exterior angle is formed by one side of the triangle and the extension of an adjacent side.
Remote interior angle is an interior angle that is not adjacent to the exterior angle.
Exterior Angle Theorem: The measure of an exterior angle of a triangle is equal to the sum of the measures of its remote interior angles.
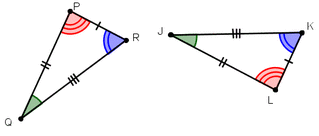
Third Angles Theorem: If two angles of one triangle are congruent to two angles of another triangle then the third pair of angles aer congruent.
Auxiliary line is a line that is added to a figure to aid in a proof.
Corollary:
4-2-2: The acute angles of a right triangle are complementary.
4-2-3: The measure of each angle of a equiangular triangle is 60 degrees.
Example: One of the acute angles in a right triangle measures 22.9 degrees. What is the measure of the other acute angle? 22.9+m=90 m=67.1.
Interior is the set of all points inside the figure.
Exterior is the set of all points outside the figure.
Interior angle is formed by two sides of a triangle.
Exterior angle is formed by one side of the triangle and the extension of an adjacent side.
Remote interior angle is an interior angle that is not adjacent to the exterior angle.
Exterior Angle Theorem: The measure of an exterior angle of a triangle is equal to the sum of the measures of its remote interior angles.
Third Angles Theorem: If two angles of one triangle are congruent to two angles of another triangle then the third pair of angles aer congruent.
Section Three: Congruent Triangle
Corresponding Angles of Polygons: Angles in the same position in two different polygons that have the same number of angles.
Corresponding Sides of Polygons: Sides in the same position in two different polygons that have the same number of sides.
Congruent Polygons: Two polygons are are congruent if and only if their corresponding angles and their sides are congruent.
Corresponding Sides of Polygons: Sides in the same position in two different polygons that have the same number of sides.
Congruent Polygons: Two polygons are are congruent if and only if their corresponding angles and their sides are congruent.
Section Four: Triangle Congruence: SSS and SAS
Triangle Rigidity: A property of triangles that states that if the side lengths of a triangle are
fixed, the triangle can have only one shape.
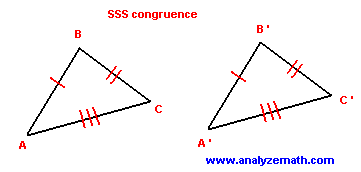
Postulate 4-4-1 (Side-Side-Side (SSS) Congruence):
If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.
Included Angle: The angle formed by two adjacent sides of a polygon.
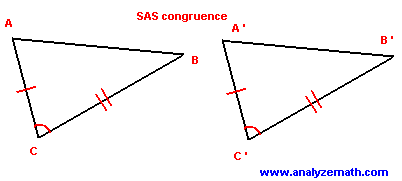
Postulate 4-4-2 ( Side-Side-Angle (SAS) Congruence):
If two side and included angles of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.
Geometry video showing Triangle Congruence (SSS and SAS) :
http://www.youtube.com/watch?v=gryB2leF6e0&feature=relmfu
fixed, the triangle can have only one shape.
Postulate 4-4-1 (Side-Side-Side (SSS) Congruence):
If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.
Included Angle: The angle formed by two adjacent sides of a polygon.
Postulate 4-4-2 ( Side-Side-Angle (SAS) Congruence):
If two side and included angles of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.
Geometry video showing Triangle Congruence (SSS and SAS) :
http://www.youtube.com/watch?v=gryB2leF6e0&feature=relmfu
Section Five: Triangle Congruence: AAS, ASA, and HL
Definitions:
Included Side: The side between two consecutive angles in a polygon.
Postulates:
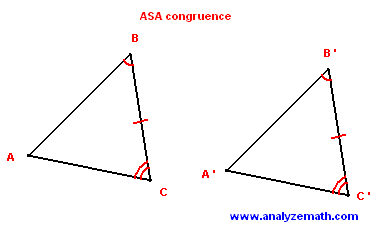
Angle-Side-Angle Congruence: If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.
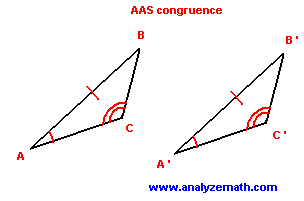
Angle-Angle Side Congruence: If two angles and a nonincluded side of one triangle are congruent to the corresponding angles and nonincluded side of another triangle, then the triangles are congruent.
Hypotenuse-Leg Congruence: If the hypotenuse and a leg of a right triangle are congruent to the hypotenuse and a leg of another right trianglem then the triangles are congruent.
Included Side: The side between two consecutive angles in a polygon.
Postulates:
Angle-Side-Angle Congruence: If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.
Angle-Angle Side Congruence: If two angles and a nonincluded side of one triangle are congruent to the corresponding angles and nonincluded side of another triangle, then the triangles are congruent.
Hypotenuse-Leg Congruence: If the hypotenuse and a leg of a right triangle are congruent to the hypotenuse and a leg of another right trianglem then the triangles are congruent.
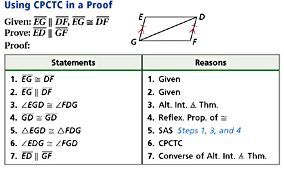
Section Six: CPCTC
CPCTC - Congruent parts of congruent triangles are congruent. This can be used as a justification in proofs.
Section Seven: Introduction to Coordinate Proof
Coordinate proof: style of proof that uses coordinate geometry and algebra.
Strategies: Use the origin as a vertex, keeping the figure in quadrant 1,center the figure at the origin, center a side of the figure at the origin, and then use one or both axes as sides of the figure.
--Proof:
Given: Right triangle ABC has vertices A(0,6) , B(0,0) , C(4,0). D is the midpoint of segment AC.
Prove: The area of figure DBC is one half the area of figure ABC.
Proof: Figure ABC is a right triangle with height AB and BC.
Area of Figure ABC= 1/2bh=1/2x4x6= 12 square units
By the midpoint formula, the coordinates of D= 0+4/2 , 6+0/2 = (2,3). The y coordinate of D is the height of Figure DBC and the base is 4 units.
Area of Figure DBC=1/2bh=1/2x4x3=6 square units
Since 12/2=6, the area of figure DBC is one half the area of figure ABC.
Strategies: Use the origin as a vertex, keeping the figure in quadrant 1,center the figure at the origin, center a side of the figure at the origin, and then use one or both axes as sides of the figure.
--Proof:
Given: Right triangle ABC has vertices A(0,6) , B(0,0) , C(4,0). D is the midpoint of segment AC.
Prove: The area of figure DBC is one half the area of figure ABC.
Proof: Figure ABC is a right triangle with height AB and BC.
Area of Figure ABC= 1/2bh=1/2x4x6= 12 square units
By the midpoint formula, the coordinates of D= 0+4/2 , 6+0/2 = (2,3). The y coordinate of D is the height of Figure DBC and the base is 4 units.
Area of Figure DBC=1/2bh=1/2x4x3=6 square units
Since 12/2=6, the area of figure DBC is one half the area of figure ABC.
Section Eight: Isosceles and Equilateral Triangles
Isosceles Triangle Theorem: If two sides of a triangle are congruent, then the angles opposite the sides are congruent.
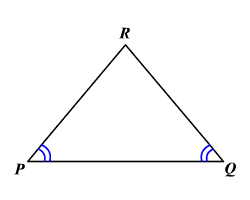
Converse of Isosceles Triangle Theorem: If two angles of a triangle are congruent, then the sides opposite those angles are congruent.
Corollary 4-8-3: Equilateral triangle: If a triangle is equilateral, then it is equiangular.
Corollary 4-8-4: Equiangular triangle: If a triangle is equiangular then it is equilateral.
Converse of Isosceles Triangle Theorem: If two angles of a triangle are congruent, then the sides opposite those angles are congruent.
Corollary 4-8-3: Equilateral triangle: If a triangle is equilateral, then it is equiangular.
Corollary 4-8-4: Equiangular triangle: If a triangle is equiangular then it is equilateral.