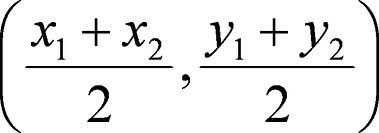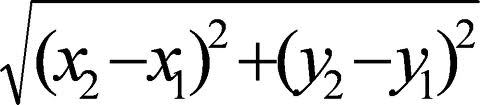Chapter One: Foundations For Geometry
Section One: Understanding Points, Lines, and Planes
Undefined Terms
Point: Names a location and has no size.
Line: A straight path that has no thickness and extends forever.
Plane: A flat surface that has no thickness and extends forever.
Definitions
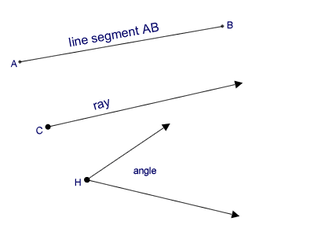
Segment: The part of a line consisting of two points and all points between them.
Endpoint: A point on one end of a segment or the starting point of a ray.
Ray: The part of a line that starts at an endpoint and extends forever in one direction.
Opposite Rays: Two rays that share the same endpoint and extend in opposite directions to form a line.
Postulates
Postulate 1-1-1: Through any two points there is exactly one line.
Postulate 1-1-2: Through any three nonlinear points there is a plane containing them.
Postulate 1-1-3: If two points lie in a plane, then the line containing those points lies in the plane.
Postulate 1-1-4: If two lines intersect, then they intersect at exactly one point.
Postulate 1-1-5: If two planes intersect, then they intersect in exactly one line.
Point: Names a location and has no size.
Line: A straight path that has no thickness and extends forever.
Plane: A flat surface that has no thickness and extends forever.
Definitions
Segment: The part of a line consisting of two points and all points between them.
Endpoint: A point on one end of a segment or the starting point of a ray.
Ray: The part of a line that starts at an endpoint and extends forever in one direction.
Opposite Rays: Two rays that share the same endpoint and extend in opposite directions to form a line.
Postulates
Postulate 1-1-1: Through any two points there is exactly one line.
Postulate 1-1-2: Through any three nonlinear points there is a plane containing them.
Postulate 1-1-3: If two points lie in a plane, then the line containing those points lies in the plane.
Postulate 1-1-4: If two lines intersect, then they intersect at exactly one point.
Postulate 1-1-5: If two planes intersect, then they intersect in exactly one line.
Section Two: Measuring And Constructing Segments
Definitions
Congruent Segments: Segments that have the same length.
Midpoint: A point that bisects a line segment in two equal segments.
Segment Bisector: Any ray, line, or segment that bisects a line segment at it’s midpoint.
Postulates
Postulate 1-2-1: The points on a line can be put in one-to-one correspondence with real numbers.
Segment Addition Postulate: If B is between A and C, then AB + BC = AC.
Congruent Segments: Segments that have the same length.
Midpoint: A point that bisects a line segment in two equal segments.
Segment Bisector: Any ray, line, or segment that bisects a line segment at it’s midpoint.
Postulates
Postulate 1-2-1: The points on a line can be put in one-to-one correspondence with real numbers.
Segment Addition Postulate: If B is between A and C, then AB + BC = AC.
Section Three: Measuring And Constructing Angles
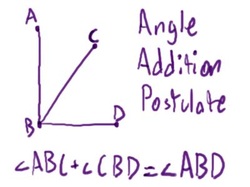
Figure A
_Definitions
Angle: Two rays that share a common endpoint.
Vertex: The common endpoint of an angle.
Acute Angle: An angle with a measure greater than 0 and less than 90.
Obtuse Angle: An angle with a measure greater than 90 and less than 180.
Right Angle: An angle with a measure of exactly 90.
Straight Angle: Formed by two opposite rays, it measures 180.
Angle Bisector: A ray that divides and angle in to two congruent angles.
Postulates
Protractor Postulate: Given line AB and point O on line AB, all rays drawn from point O can be put in to a one-to-one correspondence with real numbers 0 to 180.
Angle Addition Postulate: If point C is in the interior of <ABD, then the m<ABC+ m<CBD = m<ABD (Figure A).
Angle: Two rays that share a common endpoint.
Vertex: The common endpoint of an angle.
Acute Angle: An angle with a measure greater than 0 and less than 90.
Obtuse Angle: An angle with a measure greater than 90 and less than 180.
Right Angle: An angle with a measure of exactly 90.
Straight Angle: Formed by two opposite rays, it measures 180.
Angle Bisector: A ray that divides and angle in to two congruent angles.
Postulates
Protractor Postulate: Given line AB and point O on line AB, all rays drawn from point O can be put in to a one-to-one correspondence with real numbers 0 to 180.
Angle Addition Postulate: If point C is in the interior of <ABD, then the m<ABC+ m<CBD = m<ABD (Figure A).
Section Four: Pairs Of Angles
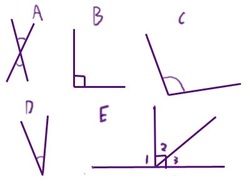
Figure B
_Definitions
Adjacent Angles: Two angles with a common side and a common vertex.
Linear Pair: A pair of adjacent angles whose non-common sides are opposite rays.
Complementary Angles: A pair of angles whose measures have a sum of 90 degrees.
Supplementary angles: A pair of angles whose measures have a sum of 180 degrees.
Vertical angles: A pair of non adjacent angles formed by two intersecting lines.
In Figure B:
A is an example of vertical angles.
B is a right angle.
C is an obtuse angle.
D is an acute angle.
E shows several things:
Angles 2 and 3 are complementary.
Angle 1 and the right angle formed by 2 and 3 are supplementary.
Adjacent Angles: Two angles with a common side and a common vertex.
Linear Pair: A pair of adjacent angles whose non-common sides are opposite rays.
Complementary Angles: A pair of angles whose measures have a sum of 90 degrees.
Supplementary angles: A pair of angles whose measures have a sum of 180 degrees.
Vertical angles: A pair of non adjacent angles formed by two intersecting lines.
In Figure B:
A is an example of vertical angles.
B is a right angle.
C is an obtuse angle.
D is an acute angle.
E shows several things:
Angles 2 and 3 are complementary.
Angle 1 and the right angle formed by 2 and 3 are supplementary.
Section Five: Using Formulas In Geometry
Definitions
Perimeter: The sum of the side lengths of a figure.
Area: The number of non overlapping square units that cover the interior of a figure.
Base: Any side of a triangle.
Height: A segment from a vertex that forms a right angle with the base.
Circumference: The distance around a circle.
Diameter: The length of a segment that passes through the center of a circle and has endpoints on the circle.
Pi: The ratio of the circumference of a circle to its diameter. It is often shown as 3.14 or 22/7.
Radius: The distance of a segment that has endpoints at the center of a circle and at any point on the circle.
Formula
Circumference of a circle: C=2(pi)r or C=(pi)d.
Area of a circle: A=(pi)r².
Area of a triangle: A=1/2bh.
Perimeter of a triangle: P=a+b+c.
Perimeter of a rectangle: 2w+2l.
Area of a rectangle: wl.
Perimeter of a square: 4s.
Area of a square: s².
Perimeter: The sum of the side lengths of a figure.
Area: The number of non overlapping square units that cover the interior of a figure.
Base: Any side of a triangle.
Height: A segment from a vertex that forms a right angle with the base.
Circumference: The distance around a circle.
Diameter: The length of a segment that passes through the center of a circle and has endpoints on the circle.
Pi: The ratio of the circumference of a circle to its diameter. It is often shown as 3.14 or 22/7.
Radius: The distance of a segment that has endpoints at the center of a circle and at any point on the circle.
Formula
Circumference of a circle: C=2(pi)r or C=(pi)d.
Area of a circle: A=(pi)r².
Area of a triangle: A=1/2bh.
Perimeter of a triangle: P=a+b+c.
Perimeter of a rectangle: 2w+2l.
Area of a rectangle: wl.
Perimeter of a square: 4s.
Area of a square: s².
Section Six: Midpoint and Distance In The Coordinate Plane
Definitions
Coordinate Plane: A plane that is divided into four quadrants by a horizontal line and a vertical line. The horizontal line is known as the x-axis. The vertical line is known as the y-axis.
Leg: The two sides that form the right angle.
Hypotenuse: The side across from the right angle that stretches from one leg to the other.
Theorems
Theorem 1-6-1: Pythagorean Theorem: In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. The formula is a squared+ b squared= c squared.
Formulas
Coordinate Plane: A plane that is divided into four quadrants by a horizontal line and a vertical line. The horizontal line is known as the x-axis. The vertical line is known as the y-axis.
Leg: The two sides that form the right angle.
Hypotenuse: The side across from the right angle that stretches from one leg to the other.
Theorems
Theorem 1-6-1: Pythagorean Theorem: In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. The formula is a squared+ b squared= c squared.
Formulas
Section Seven: Transformations In The Coordinate Planes
Definitions
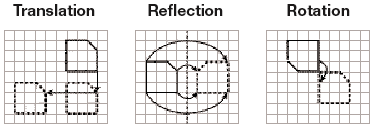
Transformation: A change in the position, size, or shape of a figure.
Preimage: The image before a transformation.
Image: The result of a transformation.
Reflection: A flip across a line called the point of reflection.
Rotation: A transformation around a point P called the center of rotation. Each point and its image are the same distance from P.
Translation: All of the points of a figure move the same distance in the same direction.
Transformation: A change in the position, size, or shape of a figure.
Preimage: The image before a transformation.
Image: The result of a transformation.
Reflection: A flip across a line called the point of reflection.
Rotation: A transformation around a point P called the center of rotation. Each point and its image are the same distance from P.
Translation: All of the points of a figure move the same distance in the same direction.