Chapter Five: Properties and Attributes of Triangles
Section One: Perpendicular and Angle Bisectors
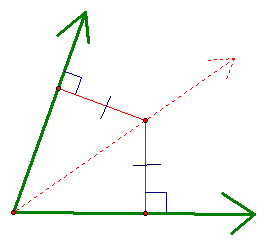
Perpendicular Bisector Theorem: If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment.
Converse of the Perpendicular Bisector Theorem: If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment,
Angle Bisector Theorem: If a point is on the bisector of an angle, then it is equidistant from the sides of the angle.
Converse of the Angle Bisector Theorem: If a point in the interior of an angle is equidistant from the sides of the angle, then it is on the bisector of the angle.
Writing equations of Bisectors in the Coordinate Plane:
1. Graph.
2. Find the midpoint.
3. Find the slope of the perpendicular bisector. Perpendicular = OPPOSITE RECIPROCAL.
4. Use the point-slope form to write an equation.
Converse of the Perpendicular Bisector Theorem: If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment,
Angle Bisector Theorem: If a point is on the bisector of an angle, then it is equidistant from the sides of the angle.
Converse of the Angle Bisector Theorem: If a point in the interior of an angle is equidistant from the sides of the angle, then it is on the bisector of the angle.
Writing equations of Bisectors in the Coordinate Plane:
1. Graph.
2. Find the midpoint.
3. Find the slope of the perpendicular bisector. Perpendicular = OPPOSITE RECIPROCAL.
4. Use the point-slope form to write an equation.
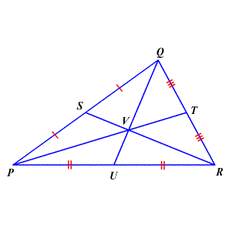
Section Three: Medians and Altitudes of Triangles
5.3 Medians and Altitudes of Triangles:
Centroid Theorem: The centroid of a triangle is located ⅔ of the distance from each vertex to the midpoint of the opposite side.
Altitude of a triangle: A perpendicular segment from a vertex to the line containing the opposite side.
Point of concurrency= orthocenter of the triangle
--Finding the Orthocenter:
1. Graph the triangle.
2. Find the equation of the line containing the altitude.
3. Find the slope of that same line. Opposite reciprocal is the slope. Put it in point-slope form.
4. Solve the system to find the coordinates of the orthocenter.
Centroid Theorem: The centroid of a triangle is located ⅔ of the distance from each vertex to the midpoint of the opposite side.
Altitude of a triangle: A perpendicular segment from a vertex to the line containing the opposite side.
Point of concurrency= orthocenter of the triangle
--Finding the Orthocenter:
1. Graph the triangle.
2. Find the equation of the line containing the altitude.
3. Find the slope of that same line. Opposite reciprocal is the slope. Put it in point-slope form.
4. Solve the system to find the coordinates of the orthocenter.
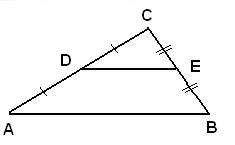
Section Four: The Triangle Midsegment Theorem
Triangle Midsegment Theorem: A midsegment of a triangle is parallel to a side of the triangle, and its length is ½ the length of that side.
Examining Midsegments in the Coordinate Plane:
1. Find the coordinates.(Midpoint Formula)
2. Compare slopes.
3. Compare the lengths. (Distance Formula)
Examining Midsegments in the Coordinate Plane:
1. Find the coordinates.(Midpoint Formula)
2. Compare slopes.
3. Compare the lengths. (Distance Formula)
Section Five: Indirect Proof and Inequalities in One Triangle
Theorem 5-5-1: If two sides of a triangle are not congruent, then the larger angle is opposite the longer side.
Theorem 5-5-2: If two angles of a triangle are not congruent, then the longer side is opposite the larger angle.
Triangle Inequality Theorem: The sum of any two sides lengths of a triangle is greater than the third side length.
AB+BC>AC
BC+AC>AB
AC+AB>BC
Example:
1. Tell whether a triangle can have sides with the given lengths.
3,5,7
3+5 >7 8>7
5+7 >3 12>3
7+3 >5 10>5
Yes the sum of each pair of lengths is greater than the third length.
Theorem 5-5-2: If two angles of a triangle are not congruent, then the longer side is opposite the larger angle.
Triangle Inequality Theorem: The sum of any two sides lengths of a triangle is greater than the third side length.
AB+BC>AC
BC+AC>AB
AC+AB>BC
Example:
1. Tell whether a triangle can have sides with the given lengths.
3,5,7
3+5 >7 8>7
5+7 >3 12>3
7+3 >5 10>5
Yes the sum of each pair of lengths is greater than the third length.
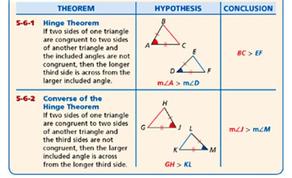
Section Six: Inequalities in Two Triangles
Hinge Theorem: If two sides of one triangle are congruent to two sides of another triangle and the included angles are not congruent, then the longer third side is across from the larger included angle.
Converse of the Hinge Theorem: If two sides of one triangle are congruent to two sides of another triangle and the third sides are not congruent, then the longer included angle is across from the longer third side.
Converse of the Hinge Theorem: If two sides of one triangle are congruent to two sides of another triangle and the third sides are not congruent, then the longer included angle is across from the longer third side.
Section Seven: The Pythagorean Theorem
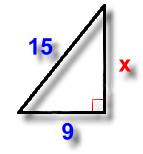
Pythagorean Theorem=a squared+b squared=c squared.
Example:
9x9=81
15x15=225
81+x=225
225-81=square root of 144 which is
12.
x=12
Example:
9x9=81
15x15=225
81+x=225
225-81=square root of 144 which is
12.
x=12
Pythagorean triple= a set of three nonzero whole numbers a,b, and c .
Common Pythagorean triples are (3,4,5), (5,12,13), (8,15,17), and (7,24,25).
Converse of the Pythagorean Theorem:
If the sum of the squares of the lengths of two sides of a triangle is equal to the square of the length of the third side, then the triangle is a right angle.
Pythagorean Inequalities Theorem:
If c squared > a squared+b squared, then the triangle is an obtuse triangle.
If c squared < a squared+b squared, then the triangle is an acute triangle.
Common Pythagorean triples are (3,4,5), (5,12,13), (8,15,17), and (7,24,25).
Converse of the Pythagorean Theorem:
If the sum of the squares of the lengths of two sides of a triangle is equal to the square of the length of the third side, then the triangle is a right angle.
Pythagorean Inequalities Theorem:
If c squared > a squared+b squared, then the triangle is an obtuse triangle.
If c squared < a squared+b squared, then the triangle is an acute triangle.
Section Eight: Applying Special Right Triangles
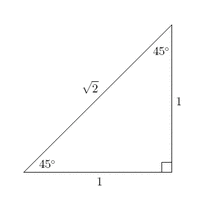
45-45-90 Triangle Theorem: In
this type of triangle, both legs are congruent, and the length of the hypotenuse
is the length of a leg times the square root of 2.
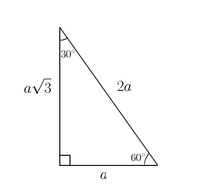
30-60-90 Triangle Theorem: The
length of the hypotenuse is 2 times the length of the shorter leg, and the
length of the longer leg is the length of the shorter leg times 3.
this type of triangle, both legs are congruent, and the length of the hypotenuse
is the length of a leg times the square root of 2.
30-60-90 Triangle Theorem: The
length of the hypotenuse is 2 times the length of the shorter leg, and the
length of the longer leg is the length of the shorter leg times 3.